Comment interpréter les signes présents sur la “carte du planétaire”

Pour garder l’attention des élèves lors de la séance de “découverte”, il est possible de fournir un dessin du planétaire. Les éléments à repérer sont rappelés dans l’item suivant. Cette liste peut être fournie en avance ou non. 

Il est intéressant de laisser les élèves chercher et de seulement indiquer qu’il reste des éléments à trouver

Les signes du planétaire sont reliés : 

      aux objets du Système Solaire (le disque 0 avec une image pour les planétaires imprimés : les planètes, la comète, parfois une planète naine, le Soleil), 

      à leurs orbites (les disques et les différentes suites numériques, les différentes couleurs)   

      à l’échelle de distance (une barre avec l’indication 1 U.A.)

      à l’échelle de durée (une phrase ou une interprétation du mouvement des objets d’un disque au suivant, voir plus loin la description de cette notion).

Il est conseillé de reprendre assez souvent les termes de position/distance et instant/durée dans les reprises des paroles des élèves ou dans les moments d’institutionnalisation (voir plus loin sur la description de la chorégraphie).

Au contraire, il est conseillé de ne pas évoquer la vitesse dans un premier temps. Tout d’abord, aucun signe sur le planétaire n’est directement relié à la vitesse. Ensuite, il y a plusieurs vitesses associées au mouvement sur le planétaire, ce qui rend son évocation complexe (voir la notion de “vitesses” plus loin).

Vous trouverez ici un “dictionnaire” des “mots du planétaire” http://planetaire.over-blog.com/2020/07/dictionnaire-planetaire.html

Pour être un objet du Système Solaire, il suffit d’avoir une orbite fermée autour du Soleil – donc de suivre une trajectoire qui “entoure” le Soleil. Le Système Solaire est constitué d’une grande variété d’objets. Selon leur masse, ils ont des noms différents.

Pour être une “comète”, un “astéroïde”, il faut être un “gros rocher”.

Pour être une planète naine, il faut être le plus gros rocher sur son orbite.

Pour être une planète rocheuse, il faut être le seul rocher sur son orbite, ce qui implique d’avoir une grande masse et d’avoir « fait le ménage sur son orbite » (tous les autres rochers ont été soit éjectés, soit intégrés à la planète, soit mis en orbite comme satellite autour de la planète).

Pour être une planète gazeuse (comme Jupiter), il faut être très massif, environ 1000 fois plus qu’une planète rocheuse !

Pour être le satellite d’une planète, il suffit de tourner autour de cette planète (et donc de suivre également son orbite autour du Soleil…)

Pour être une étoile, il faut être encore plus massif, environ 1000 fois plus qu’une planète gazeuse, au point de créer des réactions nucléaires à l’intérieur !!

Or la masse et la taille des objets ne sont pas représentées à l’échelle sur le planétaire… La seule information disponible est la présence d’orbites fermées autour d’un disque central, ce qui amène à en déduire – en connaissant le contexte – qu’il s’agit probablement d’objets du Système Solaire dans une représentation héliocentrique dans laquelle le Soleil est fixe. Il faut alors faire appel à la culture scientifique des élèves pour : décider ensemble que le disque au “centre” est le Soleil ; savoir que les orbites des planètes sont “assez circulaires” afin d’associer les premières orbites “circulaires” aux 4 planètes internes et de décider que l’objet qui a une orbite très elliptique n’est pas une planète. L’enseignant doit alors fournir le nom de la comète (Encke) qui ne peut pas être connu des élèves.

Les élèves cherchent toujours à trouver la Lune. Si votre planétaire a des dessins, alors la Lune peut ressembler à Mercure, ou à la comète…

Relances possibles : la Lune doit être proche de la Terre et tourner autour de la Terre en un mois. Aucun objet sur le planétaire ne remplit ces deux critères.

Conclusion :  la Lune n’est pas représentée… Si vous mesurez la distance Terre-Lune à l’échelle du planétaire, vous découvrirez qu’elle est située sous le disque de la Terre… 

Attention : les tailles des objets ne sont pas à l’échelle sur le planétaire. Ils ont tous le même diamètre, ce qui est faux évidemment pour les objets réels. Donc le fait que la Lune soit petite n’explique pas pourquoi elle n’est pas représentée.

Une série de disques (de même couleur ou de même forme selon les planétaires) représente les positions successives d’un objet du Système Solaire à des intervalles de temps régulier. Chaque disque correspond à la position de cet objet à un instant donné. C’est donc une chronophotographie du déplacement de cet objet le long de son orbite, sur la durée d’une révolution autour du Soleil. Dans le cas de Mercure, les disques peuvent suivre parfois deux révolutions de Mercure (voir plus loin le calcul d’une année pour chaque orbite sur le planétaire).

Si l’objet est une planète, il n’y a effectivement qu’un objet (et ses satellites) qui se déplace sur cette orbite. Si l’objet n’est pas une planète, il y a d’autres objets – plus petits – sur son orbite. 

Pour la comète, toute l’orbite est remplie de très petite poussière. Ces poussières peuvent alors entrer dans l’atmosphère de la Terre aux dates où l’orbite de la Terre et de la comète se croisent. En brûlant, ces poussières sont vues depuis le sol de la Terre et deviennent des “étoiles filantes” (si elles sont vues pendant la nuit…)

A la date indiquée sur le planétaire, tous les objets représentés étaient à la position du disque numéro 0. Cette indication permet en particulier de retrouver les saisons sur l’orbite de la Terre, et de connaître les positions des objets à toute date. Attention, les positions réelles se décalent à chaque révolution (voir la notion d’année ci-dessous)

Le choix des couleurs choisies n’est pas relié à des propriétés des différents objets. Seules les orbites de la Terre et de Mars sont généralement peintes en bleu et en rouge respectivement. Ces deux couleurs en particulier ne sont pas reliées à des différences de température (ce qui est parfois proposé par les élèves).

Les planétaires construits par les élèves ont rarement des images des planètes sur le point de départ. Au contraire, les planétaires imprimés utilisent des images réelles des différents objets. Vous pouvez alors discuter des représentations choisies sur votre planétaire. Ainsi, l’image de la Terre devrait montrer le pôle Nord (avec un faible angle) … Les parties dans l’ombre sur l’image des planètes doivent être en accord avec la direction du Soleil. Ce n’est pas toujours le cas sur certains planétaires imprimées.

L’Unité Astronomique est une distance caractéristique des longueurs dans le Système Solaire. 

Dans un premier modèle circulaire, elle correspond à la distance entre la Terre et le Soleil. Lors de la découverte du planétaire, les élèves peuvent utiliser leurs bras, leurs jambes, une corde ou une règle pour estimer la longueur de la barre d’échelle et la retrouver sur le planétaire. Ils découvriront alors que la longueur de la barre d’échelle correspond à la distance entre le Soleil et un point de la Terre. 

Dans un second modèle non circulaire ou elliptique, l’Unité Astronomique correspond à la distance moyenne entre la Terre et le Soleil. Les élèves pourront le découvrir dans la séance sur la forme des orbites avec des mesures plus précises.

Aujourd’hui, nous savons que l’orbite de la Terre n’est pas parfaitement stable. Elle se modifie légèrement, en grande partie par l’influence de Jupiter et de Saturne. La conversion entre Unité Astronomique et l’unité du mètre a alors été fixée en 2012 par l’Union Astronomique Internationale : 1 U.A. =  149 597 870 700 mètres

Sur tous les planétaires, l’unité de temps est la durée pour faire un pas.

Sur certains planétaires, l’unité de temps est indiquée (cas 1). 

Si elle n’est pas indiquée, elle est alors égale à la durée d’une année terrestre divisée par le nombre de disques sur l’orbite de la Terre (cas 2). S’il y a 24 disques, l’unité de temps est alors de 15,2 jours terrestres.

La description du Système Solaire est un modèle basé sur les observations disponibles. Ainsi, les premiers modèles – historiquement et dans le cursus scolaire – décrivent des orbites circulaires centrées sur le Soleil. Puis, la précision des mesures et la qualité des interprétations ont permis à J. Kepler de se rendre compte que les orbites sont des ellipses dont le Soleil est un des deux foyers. 

La séance sur les formes des orbites permet de faire un lien entre ce premier modèle circulaire, basé sur une première perception, et un modèle dans lequel le Soleil n’est pas le centre. Le modèle des ellipses peut alors être introduit en appliquant la “méthode du jardinier”…

(voir la séance sur les années) 

La durée d’un pas est la même pour tout le monde, tout le long de l’orbite. La durée d’une révolution sur le planétaire est donc égale à cette unité de temps multipliée par le nombre de pas.

Pour les orbites de Vénus, la Terre et Mars, le nombre de pas est égal au nombre de disques.

Sur l’orbite de Mercure, si l’unité de temps est de 16 jours (cas 1 ci-dessus), alors l’élève doit faire deux fois le tour pour revenir sur le point initial. La durée pour revenir au point initial est donc égale à deux fois une année sur Mercure… Si l’unité de temps est de 15,2 jours, alors l’orbite de Mercure ne présente pas cette difficulté.

Sur l’orbite de la comète, il faut compter 3 pas entre chaque disque.

Attention, l’année ainsi calculée sur le planétaire n’est pas égale à l’année réelle. Cette différence n’est pas dûe à une “erreur” sur le planétaire. Elle s”explique par le fait que la durée réelle du dernier pas, pour revenir à la position initiale, n’est pas nécessairement égale à l’unité de temps. Il y a alors un décalage à chaque tour entre la chorégraphie et le mouvement réel des objets. Ce décalage est égale au “reste” de la division euclidienne entre la durée réelle d’une année et le nombre de pas à effectuer pour faire un tour complet.  Le seul cas où il n’y a pas de décalage est celui de l’orbite de la Terre avec un planétaire dont l’unité de temps est égale à l’année terrestre divisée par le nombre de pas sur son orbite (cas 2 de l’unité de temps). Dans tous les autres cas, il suffit de savoir que ce décalage existe (mais reste faible et peut être ignoré…), ou d’essayer de le corriger et d’améliorer ainsi le modèle du planétaire…  C’est ce qui est fait dans le modèle de l’année avec nos calendriers pour l’année bisextile…

Dans nos calendriers, on utilise la journée comme unité de temps. Donc au bout de 365 jours, la Terre n’est pas encore revenue à son point de départ, il lui reste un quart de jour pour y arriver. Or, nous repartons quand même au 1er janvier. Cela crée un décalage entre le calendrier et la réalité. Tous les 4 ans, ce décalage est égal à un jour. Il suffit alors d’ajouter un jour du calendrier (le 29 février) pour se recaler. La Terre met toujours la même durée pour faire un tour. C’est notre calendrier qui se décale et se recale.

Toutes les planètes tournent sur elle-même, autour de leur axe de rotation, au cours de leur révolution autour du Soleil.

La durée de la révolution correspond à une année pour chaque planète (voir la séance sur les âges). 

Les durées d’une rotation et d’une révolution ne sont pas reliées. Ainsi, Mercure fait environ deux tours sur lui-même pendant une révolution, tandis que la Terre tourne 365 fois sur elle-même pendant une révolution. 

Si la durée de la rotation est bien plus petite qu’une année, elle correspond alors à l’alternance jour/nuit (c’est donc le cas pour la Terre !). Si la durée de rotation est égale à la durée de révolution, alors une moitié de la surface est toujours face au Soleil, tandis que l’autre ne voit jamais le Soleil. C’est le cas de la Lune avec la Terre : nous voyons toujours la même moitié de la surface de la Lune depuis la Terre.

Mercure, la Terre et Mars tournent autour d’elles-mêmes dans le même sens de rotation que leur mouvement autour du Soleil; tandis que Vénus tourne dans le sens opposé.

Si l’élève qui incarne la Terre veut représenter la rotation de la Terre, il.elle devra tourner 16 fois entre deux disques… Cela va rapidement le.la décourager ! Au contraire, Mercure peut essayer de tourner deux fois seulement pendant la durée de sa révolution (mais peu d’élèves le proposent…)

Vous trouverez ici un “dictionnaire” des “mots du planétaire” http://planetaire.over-blog.com/2020/07/dictionnaire-planetaire.html 

La longueur est perçue à travers la distance parcourue en allant d’un disque au suivant, donc d’une position à une autre (les lettres dans l’image ci-dessous).

Les instants sont perçus à travers le son émis. A chaque instant, un pied se pose un un disque (les images 1, 3 et 5 ci-dessous). Cela crée une impression de discontinuité qui doit être diminuée en insistant sur la durée du pas qui est continu entre deux instants (les images 2 et 4 ci-dessous). Cette durée du pas correspond au silence entre deux sons.

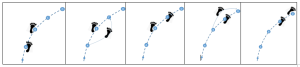
Les disques sont numérotés de 3 en 3. Un élève pourrait vouloir attendre 3 sons avant d’aller au disque suivant. Mais la comète ne peut pas attendre… Il peut donc soit faire un pas pendant la durée de 3 sons (donc il prend une durée trois fois plus longue pour faire un seul pas), ou faire trois pas pour aller au disque suivant (donc chaque pas a la même durée que tous les autres, mais il fait deux pas plus petit avant d’atteindre le disque suivant).

Le mouvement sur le planétaire peut être décrit/perçu selon plusieurs “formes” de vitesse…

La vitesse linéaire : c’est la vitesse qui relie la distance parcourue (une longueur) et la durée pour parcourir cette distance.

      La vitesse linéaire moyenne se calcule sur un trajet à partir d’une position initiale à un instant de départ jusqu’à une position finale et un instant d’arrivée. Cette vitesse est égale au rapport de la distance parcourue entre les deux positions divisée par la durée entre les deux instants. Sur le planétaire, il est possible de prendre n’importe quel couple de disque sur une orbite pour calculer cette vitesse. La durée est alors connue. Par contre, la mesure de la distance peut poser problème car le trajet exact entre deux disques n’est pas connue (ce n’est pas une ligne droite) et la position devrait être le centre des disques, mais il n’est pas (toujours) représenté..Il y a donc une incertitude dans la mesure de la distance et donc dans le calcul de la vitesse.   Sur une orbite, la vitesse linéaire moyenne est souvent calculée avec le périmètre divisé par la période.

      la vitesse linéaire instantanée est la vitesse mathématique, à un instant. Elle se calcule comme une limite de la vitesse moyenne lorsque la durée (ou la distance) tend vers zéro. Elle ne peut donc pas être calculée ainsi sur le planétaire. En supposant que les vitesses linéaires des planètes sont constantes (ce qui serait le cas pour des orbites circulaires), la vitesse linéaire instantanée correspond au coefficient directeur du graphe associant distance et durée. Ce graphe peut être construit sur le planétaire en utilisant plusieurs couples de disques sur une même orbite (ce qui est proposé dans la séance sur la vitesse). 

La vitesse angulaire. Pour la définir, il faut convenir d’un point central. Ce sera ici le Soleil. La quantité observée est alors l’angle défini par les deux demi-droites [Soleil, position de départ) et [Soleil, position d’arrivée).  La vitesse angulaire est égale au rapport entre cet angle et la durée entre les instants de départ et d’arrivée. 

   Sur une orbite, la vitesse angulaire moyenne est souvent calculée comme 360° divisée par la période.

Enfin, la vitesse ressentie par le corps est probablement une vitesse instantanée, mais il n’est pas évident de savoir s’il s’agit d’une vitesse linéaire ou angulaire, ou plutôt d’une comparaison des vitesses entre deux personnes, ou entre une personne et l’environnement. 

Le trio (vitesse, distance, durée) peut donc être associé à (vitesse linéaire, périmètre, période) ou encore (vitesse angulaire, tour complet de 360°, période). Les raisonnements des élèves vont faire référence à l’une ou à l’autre conception des vitesses, et vont faire des comparaisons de vitesse en fixant un des paramètres sur les trois (ce que l’on appelle le raisonnement linéaire causal)…

Toutes ces difficultés nous invitent à ne pas décrire les vitesses trop tôt dans l’utilisation du planétaire, et d’y consacrer une séance à part, ainsi que des exercices “préparatoires” !…