Frequently Asked Questions about the Human Orrery

A drawing of the Human Orrery can be provided to keep the pupils’ attention during the “discovery” session. The elements to be identified are listed below. This list may or may not be provided in advance.

It’s a good idea to let the students do their research and only indicate that there is still much to find.

The Human Orrery signs are in relation with:

      Solar System objects (disc 0 is made of an image for printed Orreries: planets, comets, sometimes a dwarf planet, the Sun),

      their orbits (the discs and the different numerical sequences, the different colours)  

      the distance scale (a bar marked 1 A.U.)

      the duration scale (a sentence or an interpretation of the movement of objects from one disc to the next; see below for a description of this notion).

It’s a good idea to use the terms position/distance and moment/duration often when repeating what the students have said or in the moments of institutionalisation (see below for the choreography description).

On the contrary, it is advisable to avoid mentioning speed or velocity first. No sign on the planet is directly related to speed. On the other hand, several forms of “speed” are associated with movement on the Orrery, which makes its understanding more complex (see the notion of “speeds” below).

You may find a “dictionary” of “Human Orrery words” at the bottom of the page http://planetaire.over-blog.com/en 

To be an object in the Solar System, the single requirement is to have a closed orbit around the Sun – in other words, to follow a trajectory that “goes around” the Sun. The Solar System is made up of a wide variety of objects. Depending on their mass, they have different names.

To be a “comet” or an “asteroid”, you have to be a “big rock”.

To be a dwarf planet, you have to be the biggest rock in its orbit.

To be a rocky planet, it has to be the only rock in its orbit, which means it has to have a lot of mass and to have cleaned up all other rocks in orbit (they were all either ejected or merged into one big rock, or tracked as satellites around the planet).

To be a gas planet (like Jupiter), it has to be massive, around 1000 times more massive than a rocky planet!

To be the satellite of a planet, all you have to do is orbit that planet (and therefore also follow its orbit around the Sun…).

To be a star, it has to be even more massive, about 1000 times more massive than a gaseous planet, to the point of creating nuclear reactions inside!

However, the mass and size of the objects are not represented on scale. The only information available is the presence of closed orbits around a central disc, which leads us to deduce – knowing the context – that these are probably Solar System objects in a heliocentric representation in which the Sun is fixed. You then need to call on the pupils’ scientific knowledge to: decide together that the disc at the “centre” is the Sun; know that the orbits of the planets are “fairly circular” to associate the first “circular” orbits with the four inner planets and decide that the object with a very elliptical orbit is not a planet. The teacher must then provide the comet’s name (Encke), which may not be known to the students.

Students are always trying to find the Moon. If your Orrery has drawings, the Moon may look like Mercury or a comet.

Hints: the Moon must be close to the Earth and orbit the Earth in one month. No object on the Orrery meets these two criteria.

Conclusion: The Moon is not represented. If you measure the Earth-Moon distance with the scale used for the Orrery, you will realise it is located under the Earth’s disc.

A point of attention: the sizes of the objects are not to scale on the Orrery. They all have the same diameter, which is not true for natural objects. So, the fact that the Moon is small does not explain why it is not shown.

Meteorites are rocks that come from outer space, enter the atmosphere of one planet (they are called meteors at that moment), burn (they are called shooting stars if seen during the night), and fall on the planet’s ground. So, meteorites are rocks on the ground of a planet that came from outer space. Hence, they are not on the Human Orrery.

A series of discs (of the same colour or shape, depending on the planet) represents the successive positions of an object in the Solar System at regular time intervals. Each disc corresponds to the position of that object at a given moment. It is a chronophotography of the object’s movement along its orbit throughout one revolution around the Sun. In the case of Mercury, the discs can sometimes follow two revolutions of Mercury (see below for the calculation of a year for each orbit on the planet).

If the object is a planet, only one object (and its moons) is effectively moving in that orbit. If the object is not a planet, other – smaller – objects are in its orbit.

The comet’s entire orbit is filled with tiny dust particles. Οn the dates when the Earth’s orbit and that of the comet cross, this dust can enter the Earth’s atmosphere. As it burns, this dust is seen from the Earth’s surface and becomes a “shooting star” (if seen at night).

On the date shown on the Orrery, all objects represented were at the position of disc number 0. This indication makes it possible to find the seasons in the Earth’s orbit and to know the positions of all objects at any given date. Note that the actual positions shift with each revolution (see the year concept below).

The choice of colours is unrelated to the different objects’ properties. Only the orbits of the Earth and Mars are generally painted blue and red, respectively. These two colours, in particular, are not linked to differences in temperature (as students sometimes suggest).

The Orreries constructed in school rarely have images of the planets on the starting point. On the other hand, printed planets use authentic images of the various objects. You can then discuss the representations chosen for your Orrery. For example, the image of the Earth should show the North Pole (with a slight angle). The shadow that may be observed on images of planets should be coherent with the direction of the Sun. This is only sometimes the case on some printed Orreries.

The Astronomical Unit is a distance characteristic of lengths in the Solar System.

In an initial circular model, it corresponds to the distance between the Earth and the Sun. When discovering the Orrery, students can use their arms, legs, a rope or a ruler to estimate the length of the scale bar and find it on the Orrery. They will then discover that the length of the scale bar corresponds to the distance between the Sun and a point on the Earth.

The Astronomical Unit corresponds to the average distance between the Earth and the Sun in a more sophisticated non-circular or elliptical model. Pupils can discover this in the session on the shape of orbits using more precise measurements.

We now know that the Earth’s orbit is not perfectly stable. It changes slightly, mainly due to the influence of Jupiter and Saturn. The International Astronomical Union set the conversion between the Astronomical Unit and the metre unit in 2012: 1 AU = 149,597,870,700 meters

On all planets, the unit of time is the time it takes to make one step.

On some planets, the unit of time is indicated (case 1). It is usually 16 terrestrial days.

If it is not indicated, then it is equal to the duration of one Earth year divided by the number of discs in the Earth’s orbit (case 2). If there are 24 discs, then the unit of time is 15.2 Earth days.

The description of the Solar System is a model based on available observations. The first models – historically and in the school curriculum – described circular orbits centred on the Sun. Then, the precision of the measurements and the quality of the interpretations enabled J. Kepler to realise that the orbits are ellipses with the Sun as one of the two foci.

The session on the shapes of orbits allows us to link this first circular model, based on an initial perception, and a model in which the Sun is not the centre of each orbit. Note that the Sun may be considered the centre of the Solar System. The ellipse model may be introduced by applying the “gardener’s method”…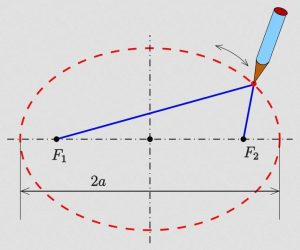

Theoretically, every orbit of the planets drawn on the HO is an ellipse. However, due to the dimension of the representation and uncertainties contained by the representation (size of the disc, thickness of the drawing, etc.), some orbits, such as the ones of Mars, Earth and Mercury, can be considered circular. Moreover, students can misjudge the circularity of the orbits following the place of the Sun or not. For example, Mercury can be considered as not circular as the Sun is not at its centre.

(see the session on years)

The duration of a step is the same for everyone along the orbit. Therefore, the duration of a revolution on the planet equals this unit of time multiplied by the number of steps.

For the orbits of Venus, Earth and Mars, the number of steps equals the number of discs.

In Mercury’s orbit, if the unit of time is 16 days (case 1 above), the student has to go around twice to return to the initial point. If the unit of time is 15.2 days (case 2), then Mercury’s orbit does not present this difficulty.

One must count three steps between each disc along the comet’s orbit.

Please note that the year calculated on the Orrery does not equal the actual year. This difference is not due to an “error” in the model of the Orrery. It is explained by the fact that the actual duration of the last step, to return to the initial position, is not necessarily equal to the unit of time. There is, therefore, a time lag at each turn between the choreography and the actual movement of the objects. This time lag is equal to the remainder of the Euclidean division between the actual duration of a year and the number of steps required to complete a full lap.  The only case where there is no offset is when the Earth orbits a planet whose unit of time is equal to the Earth’s year divided by the number of steps in its orbit (case 2 of the unit of time). In all other cases, it is sufficient to know that this offset exists but remains small and can be ignored unless one tries to predict positions over a long time. In this case, it is possible to correct it and thus improve the Orrery model. This correction is done in the model of the year with our actual calendars as one account for bissextile years.

Our calendars use the day as the unit of time. However, at the end of 365 days, the Earth has yet to return to its starting point; it still has a quarter of a day to go. Even so, we start again on 1 January after 365 days. This creates a gap between the calendar and reality. Every four years, this discrepancy is equal to one day. All we have to do is add one day to the calendar (29 February) to get back in line. The Earth always takes the same amount of time to make one revolution. It’s our calendar that shifts and shifts again.

Orbits are not all co-planar. Hence, even if the comet crosses the orbit of Earth at the exact time when Earth also crosses the orbit of the comet, there won’t be a collision since the comet is likely to be a bit above or below the plane of Earth’s orbit.

All the planets rotate on themselves, around their axis of rotation, as they revolve around the Sun.

The length of the revolution corresponds to one year for each planet (see the session on ages).

The duration of a rotation and a revolution are not related. For example, Mercury rotates about two times during one revolution, whereas the Earth rotates 365 times during one revolution.

If the duration of rotation is much shorter than one year, then it corresponds to the alternate of day and night (which is the case for the Earth!). If the duration of rotation is equal to the duration of revolution, half of the surface always faces the Sun, while the other half never sees the Sun. This is the case with the Moon’s orbit around the Earth: we always see the same half of the Moon’s surface from the Earth.

Mercury, Earth and Mars rotate around themselves in the same direction as they rotate around the Sun, while Venus rotates in the opposite direction.

If the student playing the role of the Earth wants to represent the Earth’s rotation, they will have to turn 16 times between two discs. This will quickly discourage them! Conversely, Mercury can try to rotate just twice during its revolution (but few students suggest this).

You may find a “dictionary” of “Human Orrery words“  at the bottom of the page http://planetaire.over-blog.com/en.

Length is perceived as the distance travelled from one disc to the next, i.e. from one position to another (the letters in the image below).

Moments are perceived through the sound emitted. At each moment, a foot lands on a disc (images 1, 3 and 5 below). This creates an impression of discontinuity that must be reduced by insisting on the duration of the step, which is continuous between two moments (images 2 and 4 below). This step duration corresponds to the silence between two sounds.

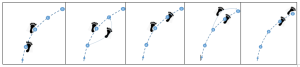
The discs are numbered three by 3. A pupil might want to wait for three sounds before moving on to the next disc. But the comet can’t wait… So he can either take one step for the duration of 3 sounds (so he takes three times as long to take one step) or take three steps to get to the next disc (so each step has the same duration as all the others, but he takes two steps shorter before reaching the next disc).

Movement on the Orrery may be described/perceived in terms of several “forms” of speed…

     Linear speed: this is the speed that links the distance travelled (a length) and the time taken to cover that distance.

     The average linear velocity is calculated over a journey from an initial position at the time of departure to a final position at the time of arrival. This speed is equal to the ratio of the distance travelled between the two positions divided by the duration between the two instants. On the Orrery, it is possible to take any pair of discs in an orbit to calculate this speed. The duration is then known. On the other hand, measuring the distance can pose a problem because the exact path between two discs is unknown (it is not a straight line), and the position should be the centre of the discs, but it needs to be (always) represented. There is, therefore, uncertainty in measuring the distance and calculating the velocity. In the case of an orbit, the mean linear velocity is often calculated with the perimeter divided by the period.

      Instantaneous linear velocity is the mathematical interpretation of velocity at a given moment. It is calculated as a limit of the average speed when time (or distance) tends towards zero. Therefore, It cannot be calculated this way on the Human Orrery. Assuming that the linear velocities of the planets are constant (which would be the case for circular orbits), the instantaneous linear velocity corresponds to the slope of the graph associating distance and time. This graph can be constructed on the Orrery using several pairs of discs in the same orbit (as proposed in the session on velocity).

      Angular velocity. To define this velocity, one needs to agree on a central point to describe an angle. This will logically be the Sun. The quantity observed is then the angle defined by the two half-lines [Sun, starting position] and [Sun, arrival position]. The angular velocity equals the ratio between this angle and the duration between the departure and arrival times. In the case of an orbit, the mean angular velocity is often calculated as 360° divided by the period.

Finally, the speed felt by the body is probably instantaneous, but it is not obvious whether it is linear or angular or a comparison of speeds between two people or between a person and the environment.

The trio (speed, distance, duration) can therefore be associated with (linear speed, perimeter, period) or even (angular speed, complete revolution of 360°, period). The student’s reasoning will refer to one or other of these concepts of speed, and they will make comparisons by fixing one of the parameters out of the three (this is known as causal linear reasoning).

All these difficulties suggest that the speeds should not be described too early in the use of the Orrery and that a separate session, along with some “preparatory or warm-up” exercises, should be devoted to this!