Συχνές Ερωτήσεις για το Μοντέλου Ηλιακού Συστήματος

Μια ζωγραφιά του Μοντέλου Ηλιακού Συστήματος μπορεί να παρασχεθεί για να κρατήσει την προσοχή των μαθητών κατά τη διάρκεια της συνεδρίας «ανακάλυψης». Τα στοιχεία που πρέπει να εντοπιστούν παρατίθενται παρακάτω. Ο κατάλογος αυτός μπορεί να παρέχεται ή να μην παρέχεται εκ των προτέρων. 

Είναι καλή ιδέα να αφήσετε τους μαθητές να κάνουν την έρευνά τους και να υποδείξετε μόνο ότι υπάρχουν ακόμη πολλά που πρέπει να βρουν. 

Τα σημάδια του Μοντέλου Ηλιακού Συστήματος βρίσκονται σε σχέση με: 

• αντικείμενα του ηλιακού συστήματος (ο δίσκος 0 αποτελείται από μια εικόνα για τυπωμένα Orreries: πλανήτες, κομήτες, μερικές φορές ένας νάνος πλανήτης, ο Ήλιος), 
• τις τροχιές τους (οι δίσκοι και οι διαφορετικές αριθμητικές ακολουθίες, τα διαφορετικά χρώματα)   
• η κλίμακα απόστασης (μια ράβδος με ένδειξη 1 A.U.)
• η κλίμακα διάρκειας (μια πρόταση ή μια ερμηνεία της κίνησης των αντικειμένων από τον ένα δίσκο στον άλλο- βλ. παρακάτω για μια περιγραφή αυτής της έννοιας).

Είναι καλή ιδέα να χρησιμοποιείτε συχνά τους όρους θέση/απόσταση και στιγμή/διάρκεια όταν επαναλαμβάνετε αυτά που είπαν οι μαθητές ή στις στιγμές της θεσμοθέτησης (βλ. παρακάτω για την περιγραφή της χορογραφίας).

Αντίθετα, καλό είναι να αποφεύγεται να αναφέρεται πρώτα η ταχύτητα ή η ταχύτητα. Κανένα σημείο στον πλανήτη δεν σχετίζεται άμεσα με την ταχύτητα. Από την άλλη πλευρά, διάφορες μορφές «ταχύτητας» συνδέονται με την κίνηση στο Μοντέλο Ηλιακού Συστήματος, γεγονός που καθιστά την κατανόησή της πιο σύνθετη (βλ. την έννοια των «ταχυτήτων» παρακάτω).

Μπορείτε να βρείτε ένα «λεξικό» των “Μοντέλου Ηλιακού Συστήματος” στο κάτω μέρος της σελίδας  http://planetaire.over-blog.com/en.

Για να είναι ένα αντικείμενο στο Ηλιακό Σύστημα, η μόνη προϋπόθεση είναι να έχει μια κλειστή τροχιά γύρω από τον Ήλιο – με άλλα λόγια, να ακολουθεί μια τροχιά που «γυρίζει» γύρω από τον Ήλιο. 

Το Ηλιακό Σύστημα αποτελείται από μια μεγάλη ποικιλία αντικειμένων. Ανάλογα με τη μάζα τους, έχουν διαφορετικά ονόματα. 

Για να είσαι «κομήτης» ή «αστεροειδής», πρέπει να είσαι «μεγάλος βράχος».

Για να είσαι νάνος πλανήτης, πρέπει να είσαι ο μεγαλύτερος βράχος στην τροχιά του.

Για να είναι ένας βραχώδης πλανήτης, πρέπει να είναι ο μοναδικός βράχος στην τροχιά του, πράγμα που σημαίνει ότι πρέπει να έχει μεγάλη μάζα και να έχει καθαρίσει όλους τους άλλους βράχους στην τροχιά του (όλοι είτε εκτινάχθηκαν είτε συγχωνεύτηκαν σε έναν μεγάλο βράχο, είτε παρακολουθούνται ως δορυφόροι γύρω από τον πλανήτη).

Για να είναι ένας αέριος πλανήτης (όπως ο Δίας), πρέπει να έχει μεγάλη μάζα, περίπου 1000 φορές μεγαλύτερη μάζα από έναν βραχώδη πλανήτη!

Για να είναι δορυφόρος ενός πλανήτη, το μόνο που πρέπει να κάνει είναι να περιφέρεται γύρω από αυτόν τον πλανήτη (και επομένως να ακολουθεί και την τροχιά του γύρω από τον Ήλιο…).

Για να είναι αστέρι, πρέπει να είναι ακόμα πιο ογκώδες, περίπου 1000 φορές πιο ογκώδες από έναν αέρινο πλανήτη, σε σημείο που να δημιουργούνται πυρηνικές αντιδράσεις στο εσωτερικό του!

Ωστόσο, η μάζα και το μέγεθος των αντικειμένων δεν αναπαρίστανται σε κλίμακα. Η μόνη διαθέσιμη πληροφορία είναι η παρουσία κλειστών τροχιών γύρω από έναν κεντρικό δίσκο, γεγονός που μας οδηγεί στο συμπέρασμα – γνωρίζοντας το πλαίσιο – ότι πρόκειται πιθανώς για αντικείμενα του Ηλιακού Συστήματος σε μια ηλιοκεντρική αναπαράσταση στην οποία ο Ήλιος είναι σταθερός. Στη συνέχεια πρέπει να επιστρατεύσετε τις επιστημονικές γνώσεις των μαθητών για να: αποφασίσουν από κοινού ότι ο δίσκος στο «κέντρο» είναι ο Ήλιος- γνωρίζουν ότι οι τροχιές των πλανητών είναι «αρκετά κυκλικές» για να συσχετίσουν τις πρώτες «κυκλικές» τροχιές με τους τέσσερις εσωτερικούς πλανήτες και να αποφασίσουν ότι το αντικείμενο με την πολύ ελλειπτική τροχιά δεν είναι πλανήτης. Ο δάσκαλος πρέπει στη συνέχεια να δώσει το όνομα του κομήτη (Encke), το οποίο μπορεί να μην είναι γνωστό στους μαθητές.

Οι μαθητές προσπαθούν πάντα να βρουν τη Σελήνη. Αν το Μοντέλου Ηλιακού Συστήματος σας έχει σχέδια, η Σελήνη μπορεί να μοιάζει με τον Ερμή ή με έναν κομήτη.

Υποδείξεις: η Σελήνη πρέπει να είναι κοντά στη Γη και να περιφέρεται γύρω από τη Γη σε ένα μήνα. Κανένα αντικείμενο στο Μοντέλου Ηλιακού Συστήματος δεν πληροί αυτά τα δύο κριτήρια.

Συμπέρασμα: Η Σελήνη δεν απεικονίζεται. Αν μετρήσετε την απόσταση Γης-Σελήνης με την κλίμακα που χρησιμοποιείται για το Μοντέλου Ηλιακού Συστήματος ,θα διαπιστώσετε ότι βρίσκεται κάτω από το δίσκο της Γης. 

Ένα σημείο προσοχής: τα μεγέθη των αντικειμένων δεν είναι σε κλίμακα στο Μοντέλου Ηλιακού Συστήματος. Όλα έχουν την ίδια διάμετρο, κάτι που δεν ισχύει για τα φυσικά αντικείμενα. Έτσι, το γεγονός ότι η Σελήνη είναι μικρή δεν εξηγεί γιατί δεν εμφανίζεται

Οι μετεωρίτες είναι πέτρες που έρχονται από το διάστημα, εισέρχονται στην ατμόσφαιρα ενός πλανήτη (εκείνη τη στιγμή ονομάζονται μετεωρίτες), καίγονται (ονομάζονται πεφταστέρια, αν παρατηρηθούν κατά τη διάρκεια της νύχτας) και πέφτουν στο έδαφος του πλανήτη. Έτσι, οι μετεωρίτες είναι πέτρες στο έδαφος ενός πλανήτη που ήρθαν από το διάστημα. Ως εκ τούτου, δεν βρίσκονται στο Μοντέλου Ηλιακού Συστήματος – Οι δίσκοι και οι τροχιές των αντικειμένων του ηλιακού συστήματος

Μια σειρά δίσκων (με το ίδιο χρώμα ή σχήμα, ανάλογα με τον πλανήτη) αναπαριστά τις διαδοχικές θέσεις ενός αντικειμένου στο Ηλιακό Σύστημα σε τακτά χρονικά διαστήματα. Κάθε δίσκος αντιστοιχεί στη θέση του εν λόγω αντικειμένου σε μια δεδομένη στιγμή. Πρόκειται για μια χρονοφωτογραφία της κίνησης του αντικειμένου κατά μήκος της τροχιάς του κατά τη διάρκεια μιας περιστροφής γύρω από τον Ήλιο. Στην περίπτωση του Ερμή, οι δίσκοι μπορούν μερικές φορές να ακολουθούν δύο περιστροφές του Ερμή (βλ. παρακάτω για τον υπολογισμό ενός έτους για κάθε τροχιά του πλανήτη).

Εάν το αντικείμενο είναι πλανήτης, μόνο ένα αντικείμενο (και τα φεγγάρια του) κινείται ουσιαστικά σε αυτή την τροχιά. Εάν το αντικείμενο δεν είναι πλανήτης, άλλα – μικρότερα – αντικείμενα βρίσκονται στην τροχιά του. 

Ολόκληρη η τροχιά του κομήτη είναι γεμάτη με μικροσκοπικά σωματίδια σκόνης. Στις ημερομηνίες που η τροχιά της Γης και του κομήτη διασταυρώνονται, η σκόνη αυτή μπορεί να εισέλθει στη γήινη ατμόσφαιρα. Καθώς καίγεται, η σκόνη αυτή γίνεται ορατή από την επιφάνεια της Γης και μετατρέπεται σε «διάττοντα αστέρα» (αν παρατηρηθεί τη νύχτα).

Μια σειρά δίσκων (με το ίδιο χρώμα ή σχήμα, ανάλογα με τον πλανήτη) αναπαριστά τις διαδοχικές θέσεις ενός αντικειμένου στο Ηλιακό Σύστημα σε τακτά χρονικά διαστήματα. Κάθε δίσκος αντιστοιχεί στη θέση του εν λόγω αντικειμένου σε μια δεδομένη στιγμή. Πρόκειται για μια χρονοφωτογραφία της κίνησης του αντικειμένου κατά μήκος της τροχιάς του κατά τη διάρκεια μιας περιστροφής γύρω από τον Ήλιο. Στην περίπτωση του Ερμή, οι δίσκοι μπορούν μερικές φορές να ακολουθούν δύο περιστροφές του Ερμή (βλ. παρακάτω για τον υπολογισμό ενός έτους για κάθε τροχιά του πλανήτη).

Εάν το αντικείμενο είναι πλανήτης, μόνο ένα αντικείμενο (και τα φεγγάρια του) κινείται ουσιαστικά σε αυτή την τροχιά. Εάν το αντικείμενο δεν είναι πλανήτης, άλλα – μικρότερα – αντικείμενα βρίσκονται στην τροχιά του. 

Ολόκληρη η τροχιά του κομήτη είναι γεμάτη με μικροσκοπικά σωματίδια σκόνης. Στις ημερομηνίες που η τροχιά της Γης και του κομήτη διασταυρώνονται, η σκόνη αυτή μπορεί να εισέλθει στη γήινη ατμόσφαιρα. Καθώς καίγεται, η σκόνη αυτή γίνεται ορατή από την επιφάνεια της Γης και μετατρέπεται σε «διάττοντα αστέρα» (αν παρατηρηθεί τη νύχτα).

Κατά την ημερομηνία που εμφανίζεται στο Μοντέλο Ηλιακού Συστήματος, όλα τα αντικείμενα που απεικονίζονται βρίσκονταν στη θέση του δίσκου με αριθμό 0. Η ένδειξη αυτή καθιστά δυνατή την εύρεση των εποχών στην τροχιά της Γης και τη γνώση των θέσεων όλων των αντικειμένων σε κάθε δεδομένη ημερομηνία. Σημειώστε ότι οι πραγματικές θέσεις μετατοπίζονται με κάθε περιστροφή (βλ. την έννοια του έτους παρακάτω).

Η επιλογή των χρωμάτων δεν σχετίζεται με τις ιδιότητες των διαφόρων αντικειμένων. Μόνο οι τροχιές της Γης και του Άρη είναι γενικά βαμμένες μπλε και κόκκινες, αντίστοιχα. Τα δύο αυτά χρώματα, ειδικότερα, δεν συνδέονται με διαφορές στη θερμοκρασία (όπως προτείνουν μερικές φορές οι μαθητές).

Τα Orreries που κατασκευάζονται στο σχολείο σπάνια έχουν εικόνες των πλανητών στην αφετηρία. Αντίθετα, οι εκτυπωμένοι πλανήτες χρησιμοποιούν αυθεντικές εικόνες των διαφόρων αντικειμένων. Μπορείτε στη συνέχεια να συζητήσετε τις αναπαραστάσεις που επιλέξατε για το δικό σας Μοντέλο Ηλιακού Συστήματος. Για παράδειγμα, η εικόνα της Γης θα πρέπει να δείχνει το Βόρειο Πόλο (με μια μικρή γωνία). Η σκιά που μπορεί να παρατηρηθεί στις εικόνες των πλανητών θα πρέπει να είναι συνεπής με την κατεύθυνση του Ήλιου. Αυτό συμβαίνει μόνο μερικές φορές σε ορισμένα τυπωμένα Orreries

Η Αστρονομική Μονάδα είναι μια απόσταση που χαρακτηρίζει τα μήκη στο Ηλιακό Σύστημα. 

Σε ένα αρχικό κυκλικό μοντέλο, αντιστοιχεί στην απόσταση μεταξύ της Γης και του Ήλιου. Κατά την ανακάλυψη του Ορράνιου, οι μαθητές μπορούν να χρησιμοποιήσουν τα χέρια τους, τα πόδια τους, ένα σχοινί ή έναν χάρακα για να εκτιμήσουν το μήκος της ράβδου κλίμακας και να το βρουν στο Ορράνιο. Στη συνέχεια θα ανακαλύψουν ότι το μήκος της ράβδου κλίμακας αντιστοιχεί στην απόσταση μεταξύ του Ήλιου και ενός σημείου της Γης. 

Η Αστρονομική Μονάδα αντιστοιχεί στη μέση απόσταση μεταξύ της Γης και του Ήλιου σε ένα πιο περίπλοκο μη κυκλικό ή ελλειπτικό μοντέλο. Οι μαθητές μπορούν να το ανακαλύψουν αυτό στη συνεδρία για το σχήμα των τροχιών χρησιμοποιώντας πιο ακριβείς μετρήσεις.

Γνωρίζουμε τώρα ότι η τροχιά της Γης δεν είναι απόλυτα σταθερή. Μεταβάλλεται ελαφρώς, κυρίως λόγω της επιρροής του Δία και του Κρόνου. Η Διεθνής Αστρονομική Ένωση καθόρισε τη μετατροπή μεταξύ της Αστρονομικής Μονάδας και της μονάδας του μέτρου το 2012: 1 AU = 149.597.870.700 μέτρα.

Σε όλους τους πλανήτες, η μονάδα του χρόνου είναι ο χρόνος που χρειάζεται για να κάνει κανείς ένα βήμα.

Σε ορισμένους πλανήτες, η μονάδα του χρόνου αναφέρεται (περίπτωση 1). Συνήθως είναι 16 γήινες ημέρες.

Εάν δεν αναφέρεται, τότε ισούται με τη διάρκεια ενός γήινου έτους διαιρεμένη με τον αριθμό των δίσκων της γήινης τροχιάς (περίπτωση 2). Εάν υπάρχουν 24 δίσκοι, τότε η μονάδα του χρόνου είναι 15,2 γήινες ημέρες.

Η περιγραφή του ηλιακού συστήματος είναι ένα μοντέλο που βασίζεται στις διαθέσιμες παρατηρήσεις. Τα πρώτα μοντέλα – ιστορικά και στο σχολικό πρόγραμμα σπουδών – περιέγραφαν κυκλικές τροχιές με κέντρο τον Ήλιο. Στη συνέχεια, η ακρίβεια των μετρήσεων και η ποιότητα των ερμηνειών επέτρεψαν στον J. Kepler να συνειδητοποιήσει ότι οι τροχιές είναι ελλείψεις με τον Ήλιο ως μία από τις δύο εστίες. 

Η συνεδρία για τα σχήματα των τροχιών μας επιτρέπει να συνδέσουμε αυτό το πρώτο κυκλικό μοντέλο, που βασίζεται σε μια αρχική αντίληψη, με ένα μοντέλο στο οποίο ο Ήλιος δεν είναι το κέντρο κάθε τροχιάς. Σημειώστε ότι ο Ήλιος μπορεί να θεωρηθεί το κέντρο του ηλιακού συστήματος. Το μοντέλο της έλλειψης μπορεί να εισαχθεί με την εφαρμογή της «μεθόδου του κηπουρού»...

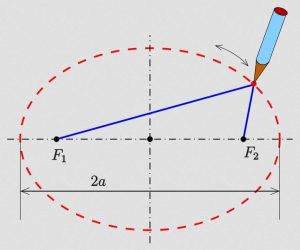
Θεωρητικά, κάθε τροχιά των πλανητών που σχεδιάζεται στο Μοντέλο Ηλιακού Συστήματος είναι μια έλλειψη. Ωστόσο, λόγω της διάστασης της αναπαράστασης και των αβεβαιοτήτων που περιέχει η αναπαράσταση (μέγεθος του δίσκου, πάχος του σχεδίου κ.λπ.), ορισμένες τροχιές, όπως αυτές του Άρη, της Γης και του Ερμή, μπορούν να θεωρηθούν κυκλικές. Επιπλέον, οι μαθητές μπορούν να κρίνουν λανθασμένα την κυκλικότητα των τροχιών που ακολουθούν τη θέση του Ήλιου ή όχι. Για παράδειγμα, ο Ερμής μπορεί να θεωρηθεί μη κυκλικός καθώς ο Ήλιος δεν βρίσκεται στο κέντρο του.

Η διάρκεια ενός βήματος είναι η ίδια για όλους κατά μήκος της τροχιάς. Επομένως, η διάρκεια μιας περιστροφής στον πλανήτη ισούται με αυτή τη μονάδα χρόνου πολλαπλασιασμένη επί τον αριθμό των βημάτων.

Για τις τροχιές της Αφροδίτης, της Γης και του Άρη, ο αριθμός των βημάτων ισούται με τον αριθμό των δίσκων.

Στην τροχιά του Ερμή, αν η μονάδα χρόνου είναι 16 ημέρες (περίπτωση 1 παραπάνω), ο μαθητής πρέπει να κάνει δύο φορές το γύρο του για να επιστρέψει στο αρχικό σημείο. Αν η μονάδα του χρόνου είναι 15,2 ημέρες (περίπτωση 2), τότε η τροχιά του Ερμή δεν παρουσιάζει αυτή τη δυσκολία.

Πρέπει να μετρήσει κανείς τρία βήματα μεταξύ κάθε δίσκου κατά μήκος της τροχιάς του κομήτη.

Σημειώστε ότι το έτος που υπολογίζεται στο Μοντέλο Ηλιακού Συστήματος δεν είναι ίσο με το πραγματικό έτος. Η διαφορά αυτή δεν οφείλεται σε «σφάλμα» στο μοντέλο του Μοντέλου Ηλιακού Συστήματος. Εξηγείται από το γεγονός ότι η πραγματική διάρκεια του τελευταίου βήματος, για την επιστροφή στην αρχική θέση, δεν είναι απαραίτητα ίση με τη μονάδα του χρόνου. Υπάρχει, επομένως, μια χρονική υστέρηση σε κάθε στροφή μεταξύ της χορογραφίας και της πραγματικής κίνησης των αντικειμένων. Αυτή η χρονική υστέρηση είναι ίση με το υπόλοιπο της ευκλείδειας διαίρεσης μεταξύ της πραγματικής διάρκειας ενός έτους και του αριθμού των βημάτων που απαιτούνται για τη συμπλήρωση ενός πλήρους γύρου.  Η μόνη περίπτωση όπου δεν υπάρχει μετατόπιση είναι όταν η Γη περιφέρεται γύρω από έναν πλανήτη του οποίου η μονάδα χρόνου είναι ίση με το έτος της Γης διαιρεμένο με τον αριθμό των βημάτων της τροχιάς του (περίπτωση 2 της μονάδας χρόνου). Σε όλες τις άλλες περιπτώσεις, αρκεί να γνωρίζουμε ότι το offset αυτό υπάρχει, αλλά παραμένει μικρό και μπορεί να αγνοηθεί, εκτός αν κάποιος προσπαθεί να προβλέψει θέσεις για μεγάλο χρονικό διάστημα… Σε αυτή την περίπτωση, είναι δυνατόν να διορθωθεί και έτσι να βελτιωθεί το μοντέλο Μοντέλο Ηλιακού Συστήματος. Αυτή η διόρθωση γίνεται στο μοντέλο του έτους με τα πραγματικά μας ημερολόγια, καθώς ένας λογαριασμός για τα δίσεκτα έτη.

Τα ημερολόγιά μας χρησιμοποιούν την ημέρα ως μονάδα του χρόνου. Ωστόσο, στο τέλος των 365 ημερών, η Γη δεν έχει ακόμη επιστρέψει στο σημείο εκκίνησής της- έχει ακόμη ένα τέταρτο της ημέρας να διανύσει. Ακόμα κι έτσι, ξεκινάμε ξανά την 1η Ιανουαρίου μετά από 365 ημέρες. Αυτό δημιουργεί ένα κενό μεταξύ του ημερολογίου και της πραγματικότητας. Κάθε τέσσερα χρόνια, η διαφορά αυτή ισούται με μία ημέρα. Το μόνο που έχουμε να κάνουμε είναι να προσθέσουμε μία ημέρα στο ημερολόγιο (29 Φεβρουαρίου) για να επανέλθουμε στην πραγματικότητα. Η Γη χρειάζεται πάντα τον ίδιο χρόνο για να κάνει μια περιστροφή. Το ημερολόγιό μας είναι αυτό που μετατοπίζεται και μετατοπίζεται ξανά και ξανά. 

Οι τροχιές δεν είναι όλες συνεπίπεδες. Ως εκ τούτου, ακόμη και αν ο κομήτης διασχίσει την τροχιά της Γης ακριβώς τη στιγμή που η Γη διασχίζει επίσης την τροχιά του κομήτη, δεν θα υπάρξει σύγκρουση, αφού ο κομήτης είναι πιθανό να βρίσκεται λίγο πάνω ή κάτω από το επίπεδο της τροχιάς της Γης.

Όλοι οι πλανήτες περιστρέφονται γύρω από τον εαυτό τους, γύρω από τον άξονα περιστροφής τους, καθώς περιστρέφονται γύρω από τον Ήλιο.

Το μήκος της περιστροφής αντιστοιχεί σε ένα έτος για κάθε πλανήτη (βλ. την ενότητα για τις ηλικίες). 

Η διάρκεια μιας περιστροφής και μιας περιστροφής δεν σχετίζονται μεταξύ τους. Για παράδειγμα, ο Ερμής περιστρέφεται περίπου δύο φορές κατά τη διάρκεια μιας περιστροφής, ενώ η Γη περιστρέφεται 365 φορές κατά τη διάρκεια μιας περιστροφής. 

Αν η διάρκεια της περιστροφής είναι πολύ μικρότερη από ένα έτος, τότε αντιστοιχεί στην εναλλαγή ημέρας και νύχτας (πράγμα που ισχύει για τη Γη!). Αν η διάρκεια της περιστροφής είναι ίση με τη διάρκεια της περιστροφής, η μισή επιφάνεια της Γης βλέπει πάντα τον Ήλιο, ενώ η άλλη μισή δεν βλέπει ποτέ τον Ήλιο. Αυτό συμβαίνει με την τροχιά της Σελήνης γύρω από τη Γη: βλέπουμε πάντα το ίδιο μισό της επιφάνειας της Σελήνης από τη Γη.

Ο Ερμής, η Γη και ο Άρης περιστρέφονται γύρω από τον εαυτό τους προς την ίδια κατεύθυνση που περιστρέφονται γύρω από τον Ήλιο, ενώ η Αφροδίτη περιστρέφεται προς την αντίθετη κατεύθυνση.

Αν ο μαθητής που παίζει το ρόλο της Γης θέλει να αναπαραστήσει την περιστροφή της Γης, θα πρέπει να γυρίσει 16 φορές ανάμεσα σε δύο δίσκους. Αυτό θα τους αποθαρρύνει γρήγορα! Αντίθετα, ο Ερμής μπορεί να προσπαθήσει να περιστραφεί μόνο δύο φορές κατά τη διάρκεια της περιστροφής του (αλλά λίγοι μαθητές το προτείνουν αυτό).

Μπορείτε να βρείτε ένα «λεξικό» των «λέξεων του Μοντέλου Ηλιακού Συστήματος» στο κάτω μέρος της σελίδας http://planetaire.over-blog.com/en.

Το μήκος γίνεται αντιληπτό ως η απόσταση που διανύεται από τον ένα δίσκο στον άλλο, δηλαδή από τη μια θέση στην άλλη (τα γράμματα στην παρακάτω εικόνα).

Οι στιγμές γίνονται αντιληπτές μέσω του ήχου που εκπέμπεται. Σε κάθε στιγμή, ένα πόδι προσγειώνεται σε έναν δίσκο (εικόνες 1, 3 και 5 παρακάτω). Αυτό δημιουργεί μια εντύπωση ασυνέχειας που πρέπει να μειωθεί με την επιμονή στη διάρκεια του βήματος, η οποία είναι συνεχής μεταξύ δύο στιγμών (εικόνες 2 και 4 παρακάτω). Αυτή η διάρκεια του βήματος αντιστοιχεί στη σιωπή μεταξύ δύο ήχων.

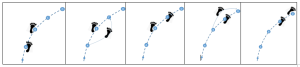
Οι δίσκοι είναι αριθμημένοι τρεις προς 3. Ένας μαθητής μπορεί να θέλει να περιμένει τρεις ήχους πριν προχωρήσει στον επόμενο δίσκο. Αλλά ο κομήτης δεν μπορεί να περιμένει… Έτσι μπορεί είτε να κάνει ένα βήμα για τη διάρκεια των 3 ήχων (άρα χρειάζεται τρεις φορές περισσότερη ώρα για να κάνει ένα βήμα) είτε να κάνει τρία βήματα για να φτάσει στον επόμενο δίσκο (άρα κάθε βήμα έχει την ίδια διάρκεια με όλα τα άλλα, αλλά κάνει δύο βήματα μικρότερα πριν φτάσει στον επόμενο δίσκο).

Η μετακίνηση στο Μοντέλου Ηλιακού Συστήματος μπορεί να περιγράφει/αντιληφθεί με όρους διαφόρων «μορφών» ταχύτητας…

Γραμμική ταχύτητα: αυτή είναι η ταχύτητα που συνδέει τη διανυόμενη απόσταση (ένα μήκος) και το χρόνο που απαιτείται για να καλυφθεί η απόσταση αυτή.

     Η μέση γραμμική ταχύτητα υπολογίζεται κατά τη διάρκεια μιας διαδρομής από μια αρχική θέση τη στιγμή της αναχώρησης σε μια τελική θέση τη στιγμή της άφιξης. Η ταχύτητα αυτή ισούται με το λόγο της διανυθείσας απόστασης μεταξύ των δύο θέσεων δια της διάρκειας μεταξύ των δύο χρονικών στιγμών. Στο Μοντέλου Ηλιακού Συστήματος, είναι δυνατόν να ληφθεί οποιοδήποτε ζεύγος δίσκων σε τροχιά για τον υπολογισμό αυτής της ταχύτητας. Η διάρκεια είναι τότε γνωστή. Από την άλλη πλευρά, η μέτρηση της απόστασης μπορεί να δημιουργήσει πρόβλημα, επειδή η ακριβής διαδρομή μεταξύ δύο δίσκων είναι άγνωστη (δεν είναι ευθεία γραμμή), και η θέση θα πρέπει να είναι το κέντρο των δίσκων, αλλά πρέπει να αναπαρίσταται (πάντα). Επομένως, υπάρχει αβεβαιότητα στη μέτρηση της απόστασης και στον υπολογισμό της ταχύτητας.    

Η στιγμιαία γραμμική ταχύτητα είναι η μαθηματική ερμηνεία της ταχύτητας σε μια δεδομένη στιγμή. Υπολογίζεται ως όριο της μέσης ταχύτητας όταν ο χρόνος (ή η απόσταση) τείνει προς το μηδέν. Επομένως, δεν μπορεί να υπολογιστεί με αυτόν τον τρόπο στο Μοντέλο Ηλιακού Συστήματος Υποθέτοντας ότι οι γραμμικές ταχύτητες των πλανητών είναι σταθερές (κάτι που θα συνέβαινε για κυκλικές τροχιές), η στιγμιαία γραμμική ταχύτητα αντιστοιχεί στην κλίση του διαγράμματος που συνδέει την απόσταση και το χρόνο. Αυτή η γραφική παράσταση μπορεί να κατασκευαστεί στο Μοντέλου Ηλιακού Συστήματος χρησιμοποιώντας πολλά ζεύγη δίσκων στην ίδια τροχιά (όπως προτάθηκε στη συνεδρία για την ταχύτητα). 

      Γωνιακή ταχύτητα. Για να ορίσουμε αυτή την ταχύτητα, πρέπει να συμφωνήσουμε σε ένα κεντρικό σημείο για να περιγράψουμε μια γωνία. Αυτό λογικά θα είναι ο Ήλιος. Η παρατηρούμενη ποσότητα είναι τότε η γωνία που ορίζεται από τις δύο ημιευθείες [Ήλιος, θέση εκκίνησης] και [Ήλιος, θέση άφιξης]. Η γωνιακή ταχύτητα ισούται με το λόγο μεταξύ αυτής της γωνίας και της διάρκειας μεταξύ των χρόνων αναχώρησης και άφιξης. Στην περίπτωση μιας τροχιάς, η μέση γωνιακή ταχύτητα υπολογίζεται συχνά ως 360° διαιρεμένη με την περίοδο.

Τέλος, η ταχύτητα που αισθάνεται το σώμα είναι πιθανότατα στιγμιαία, αλλά δεν είναι προφανές αν είναι γραμμική ή γωνιακή ή μια σύγκριση των ταχυτήτων μεταξύ δύο ατόμων ή μεταξύ ενός ατόμου και του περιβάλλοντος

Το τρίο (ταχύτητα, απόσταση, διάρκεια) μπορεί επομένως να συσχετιστεί με (γραμμική ταχύτητα, περίμετρος, περίοδος) ή ακόμη και με (γωνιακή ταχύτητα, πλήρης περιστροφή 360°, περίοδος). Ο συλλογισμός του μαθητή θα αναφέρεται στη μία ή την άλλη από αυτές τις έννοιες της ταχύτητας και θα κάνει συγκρίσεις καθορίζοντας μία από τις τρεις παραμέτρους (αυτό είναι γνωστό ως αιτιώδης γραμμικός συλλογισμός).

Όλες αυτές οι δυσκολίες υποδηλώνουν ότι οι ταχύτητες δεν πρέπει να περιγράφονται πολύ νωρίς κατά τη χρήση του Μοντέλου Ηλιακού Συστήματος και ότι μια ξεχωριστή συνεδρία, μαζί με κάποιες ασκήσεις «προετοιμασίας ή προθέρμανσης», πρέπει να αφιερωθεί σε αυτό!